Công thức tính diện tích hình bình hành
Trong hình học có rất nhiều hình khác nhau và mỗi hình có một dấu hiệu nhận biết nhất định, có những tính chất đặc thù của mỗi hình và công thức tính chu vi, diện tích khác nhau. Một trong những hình khá khó trong hình học đó là hình bình hành vì nó có một số đặc điểm trùng với các hình khác như hình thang đặc biệt hay hình chữ nhật. Bài viết sau đây sẽ giúp bạn có cái nhìn tổng quát hơn về hình bình hành cũng như công thức tính diện tích hình bình hành.
1. Khái quát về hình bình hành
Theo Wikipedia, hình bình hành trong hình học Euclide là một hình tứ giác được tạo thành khi hai cặp đường thẳng song song cắt nhau. Nó là một dạng đặc biệt của hình thang (hình thang có hai cạnh bên song song)
Bạn đang xem: Công thức tính diện tích hình bình hành
Nếu ta nói hình bình hành ABCD thì ta sẽ hình dung như sau: AB//CD, AD//BC và AB= CD, AD= BC. Gọi AC và BD là hai đường chéo cắt nhau tại E thì EA= EC và ED= EB.
– Một số tính chất của hình bình hành: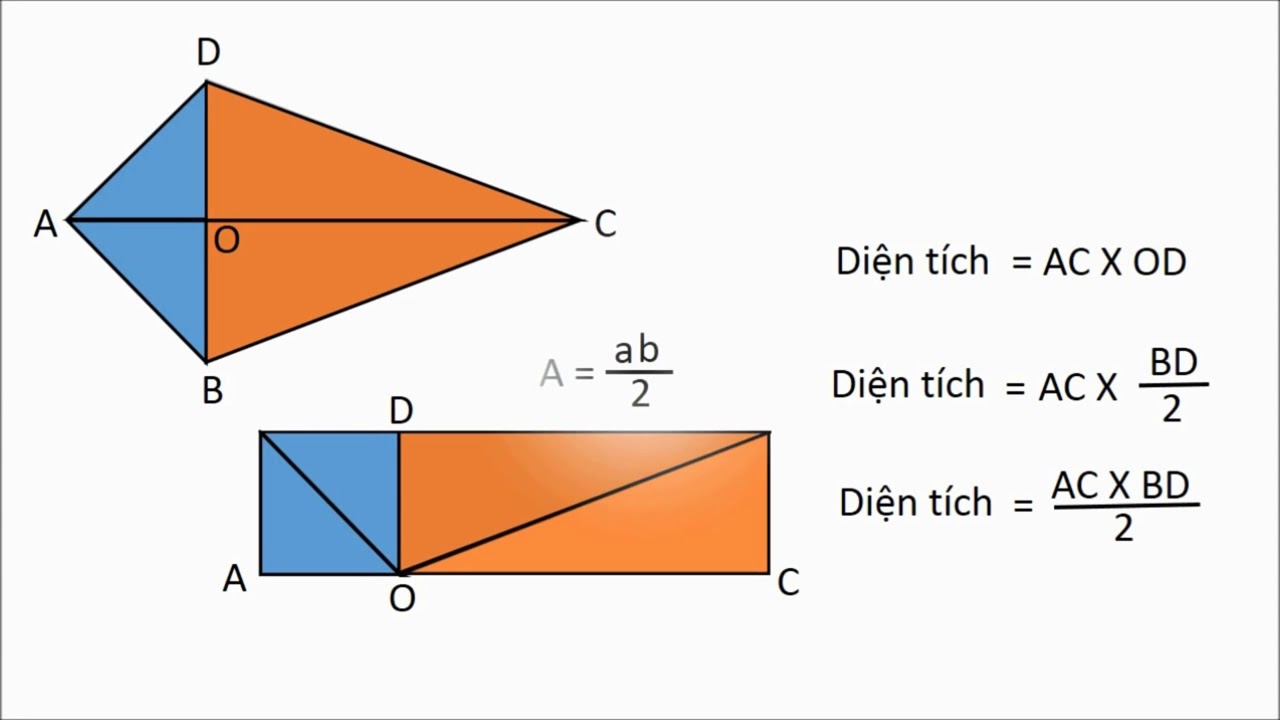
- Các cặp cạnh đối song song và bằng nhau, hai cạnh liền kề không tạo thành góc vuông.
- Các góc đối của hình bình hành thì bằng nhau.
- Hai đường chéo của hình bình hành cắt nhau tại trung điểm của mỗi đường.
– Dấu hiệu nhận biết của hình bình hành, có năm dấu hiệu chính như sau:
- Một tứ giác mà có hai cặp cạnh đối song song là hình bình hành.
- Một tứ giác mà có các cạnh đối bằng nhau là hình bình hành.
- Một tứ giác mà có hai cạnh đối vừa song song và vừa bằng nhau là hình bình hành.
- Một tứ giác mà có các góc đối bằng nhau thì là hình bình hành.
Một tứ giác mà có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Vì là một dạng đặc biệt của hình thang, do đó, ngoài những tính chất ở trên thì hình bình hành còn có những tính chất của hình thang như tính chất về góc: Trong hình bình hành, hai góc trong kề một cạnh bên của hình bình hành có tổng bằng 180 độ. Ví dụ: hình bình hành ABCD có AB//CD, AD và BC là hai cạnh bên thì góc BAD + ADC = 180 độ.
Dạng đặc biệt của hình bình hành chính là hình chữ nhật, hay còn gọi là hình bình hành có một góc vuông chính là hình chữ nhật.
2. Công thức tính diện tích hình bình hành và ví dụ minh họa
Nếu chu vi hình bình hành đơn giản là cộng bốn cạnh của hình bình hành lại với nhau hoặc tóm gọn lại bằng công thức tổng độ dài hai cạnh liền kề sau đó nhân 2 thì công thức tính diện tích hình bình hành như sau:
Muốn tính diện tích hình bình hành, ta lấy độ dài một cạnh đáy nhân với chiều cao tương ứng: S= axh
Trong đó:
- S là diện tích hình bình hành, đơn vị là cm2 ( hoặc dm2, m2)
- a là độ dài cạnh đáy
- h là độ dài đường cao hạ xuống cạnh đáy a.
Nếu bạn thấy công thức này quá khó nhớ hay dễ nhầm lẫn với các công thức tính diện tích các hình khác thì bạn có thể học thuộc những câu thơ dưới đây:
Xem thêm : Công thức tính đạo hàm và các đạo hàm thông dụng
“Bình Hành Diện Tích không sai
Chiều cao nhân đáy ai ai cũng làm”
Hoặc bài thơ khác:
“Diện Tích Của Hình Bình Hành
Chiều cao nhân đáy là thành ngay thôi”
Hoặc:
“Muốn tìm diện tích bình hành
Chiều cao nhân đáy rành rành phải ghi”
Những câu thơ này là do kinh nghiệm của các thầy cô, các thế hệ trước truyền lại cho nhau và nếu học thuộc nó bạn có thể áp dụng một cách dễ dàng, khó nhầm lẫn với các công thức khác.
Để hiểu rõ hơn về công thức tính diện tích hình bình hành, sau đây là một số ví dụ về tính diện tích hình bình hành: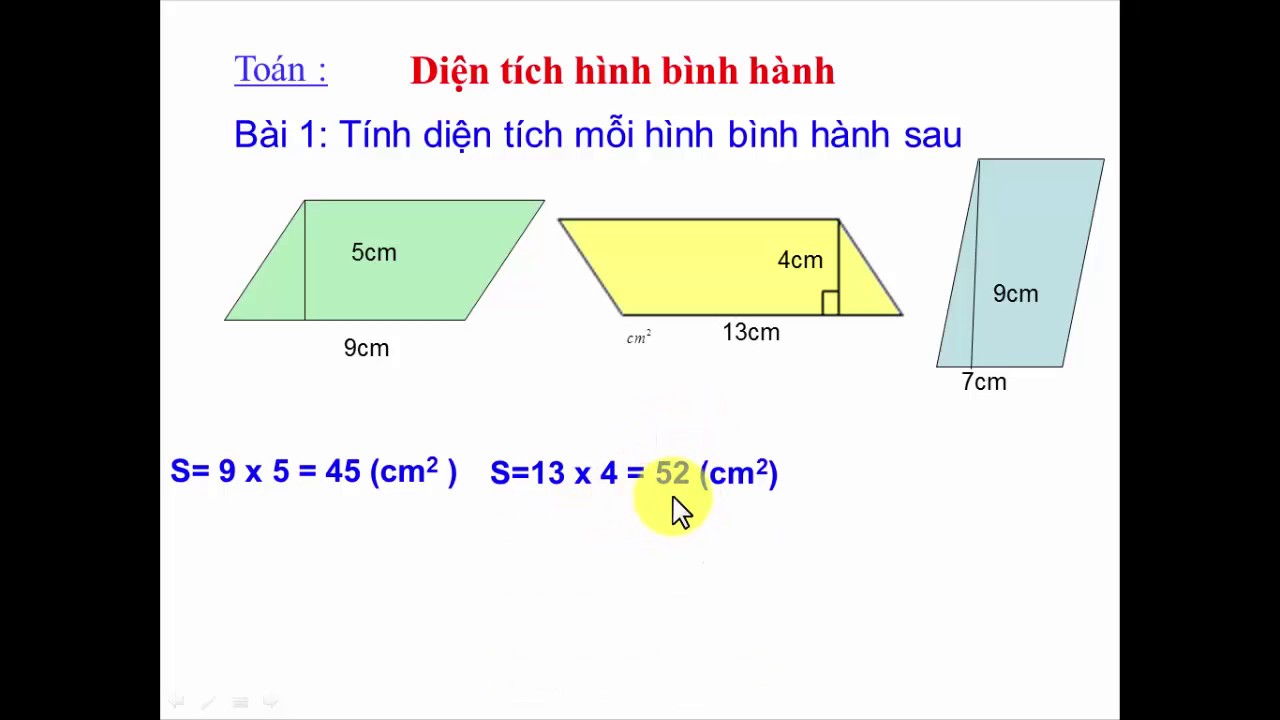
Ví dụ 1: Cho hình bình hành ABCD, từ A kẻ một đường vuông góc với CD tại điểm H và AH= 6 cm, CD = 7 cm. Tính diện tích hình bình hành ABCD.
Ta có AH vuông góc với CD, do đó, AH chính là đường cao hạ xuống đáy CD.
Diện tích hình bình hành ABCD: SABCD= axh = AHx CD= 6×7= 42 cm2.
Xem thêm : Công thức tính chu vi hình tròn nhanh và chính xác nhất
Ví dụ 2: Tính diện tích một thửa ruộng hình bình hành có chiều cao là 50m và độ dài cạnh đáy gấp đôi chiều cao.
Bài toán đã cho chiều cao thửa ruộng hình bình hành là 50m, do đó ta cần tìm độ dài của cạnh đáy.
Theo bài ra, độ dài cạnh đáy a gấp đôi chiều cao h, suy ra a=2h= 2x 50= 100m
Diện tích thửa ruộng hình bình hành là: S=axh= 50×100= 5000 m2.
Đáp số: 5000 m2
Ví dụ 3: Tính diện tích hình bình hành MNPQ biết cạnh đáy PQ = 9 cm và chiều cao MH bằng 2/3 đáy.
Đối với bài toán này, dữ liệu đã biết chính là cạnh đáy PQ= 9 cm, ta cần tìm dữ liệu còn lại là chiều cao MH.
Ta có MH bằng 2/3 đáy tức là MH= 2/3PQ= 2/3 x 9 cm= 6 cm.
Ta có công thức tính diện tích hình bình hành MNPQ như sau:
SMNPQ= PQx MH= 9 x 6 = 54 cm2
Đáp số: 54 cm2
Như vậy, bài viết trên đã giúp bạn hiểu rõ hơn về hình bình hành, một số tính chất quan trọng cũng như công thức tính diện tích hình bình hành. Chúc các bạn học tốt và đạt nhiều kết quả cao trong học tập.
Nguồn: https://www.nhomai.vn
Danh mục: Công Thức