Công thức tính đạo hàm và các đạo hàm thông dụng
Khi học lên đến bậc trung học phổ thông chắc hẳn lượng kiến thức các bạn nhận được là rất lớn, bên cạnh đó những công thức của các môn học khá nhiều khiến bạn cảm thấy căng thẳng mỗi khi muốn tìm đến một công thức nào đó để giải quyết đống bài tập của mình. Chính bởi những nguyên nhân này mà bài viết hôm nay chúng tôi sẽ giới thiệu chi tiết đến các bạn về công thức tính đạo hàm. Mời các bạn theo dõi bài viết dưới đây nhé!
1. Tìm hiểu về đạo hàm
1.1. Khái niệm
Đạo hàm là một hàm số đóng vai trò quan trọng trong việc tính toán. Ta có thể hiểu đơn giản đạo hàm của một hàm số chính là việc mô tả lại sự biến thiên của hàm số đó tại một điểm bất kỳ.
Bạn đang xem: Công thức tính đạo hàm và các đạo hàm thông dụng
Đạo hàm có biểu diễn trong hình học là hệ số góc của tiếp tuyến với đồ thị biểu diễn hàm số. Về vật lý, đạo hàm biểu diễn vận tốc tức thời của một chất điểm chuyển động hoặc cường độ dòng điện tức thời tại một điểm trên dây dẫn.
1.2. Quy tắc đạo hàm
+ Quy tắc cơ bản của đạo hàm:
Đạo hàm của hằng số bằng 0. Ký hiệu: ( C )’ = 0
Đạo hàm của một tổng bằng tổng các đạo hàm.
Ký hiệu: ( u + v )’ = ( u )’ + ( v )’ hoặc ( u1 + u2 + u3 + …+ Un )’ = ( u1 )’ + ( u2)’ + (u3)’ +… + (Un)’
Đạo hàm của hàm số nhân ( u * v )’ = ( u )’*v + ( v )’*u
Đạo hàm của hàm số chia ( u/v )’ = (( u )’*v – ( v )’*u )/ v^2
+ Quy tắc đạo hàm của hàm số hợp:
Nếu y = y(u(x)) thì y’(x) = y’(u) * u’(x)
1.3. Ý nghĩa của đạo hàm
Về hình học:
Đạo hàm của hàm số f(x) tại điểm x0x0 là hệ số góc của tiếp tuyến tại điểm M(x0,f(x0)) M(x0,f(x0)) đó.
=> Phương trình của tiếp tuyến tại điểm M: y−y0=f′(x0)(x−x0)y−y0=f′(x0)(x−x0)
Về vật lý:
Khi xét chuyển động thẳng s=f(t)s=f(t)
Lúc này vận tốc tức thời tại thời điểm t0t0 là: v(t0)=s′(t0)=f′(t0)v(t0)=s′(t0)=f′(t0)
Còn gia tốc tức thời tại thời điểm t0t0 là đạo hàm cấp 2 của phương trình chuyển động:
a(t0)= f′′(t0) a(t0)=f″(t0)
Giả sử điện lượng Q truyền trong dây dẫn xác định bởi phương trình:
Q=f(t)Q=f(t)
Cường độ tức thời của dòng điện tại thời điểm t0t0: I(t0)=Q′(t0)=f′(t0)
2. Công thức tính đạo hàm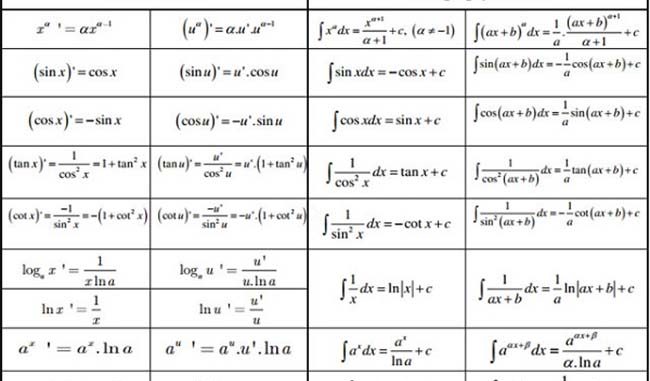
Nếu như để ý các bạn sẽ thấy được việc tìm kiếm thông tin về công thức tính đạo hàm trên các trang mạng rất đa dạng và phong phú từ những công thức đơn giản đến những công thức nâng cao. Dưới đây, chúng tôi cũng đã tổng hợp được các công thức tính đạo hàm từ đơn giản đến nâng cao cho các bạn tiện tham khảo, cụ thể là:
2.1. Các công thức tính đạo hàm cơ bản
Xem thêm : Điều cần biết về công thức tính nồng độ mol
Hàm số y=xn(n∈N,n>1) có đạo hàm với mọi x∈R và: (xn)′=nxn–1.
Dựa vào công thức tính đạo hàm ta có nhận xét sau:
(C)’= 0 (với C là hằng số).
(x)’=1.
2.2. Đạo hàm trong các phép toán của hàm số
Cho u=u(x)vàv=v(x) lần lượt là các hàm số có đạo hàm tại điểm x, ta có công thức sau:
(u+v)′=u′+v′;
(u–v)′=u′–v′;
(u.v)′=u′.v+u.v′;
(u/v)′=u′v−uv′/v2,(v(x)≠0)
2.3. Công thức mở rộng cho các hàm số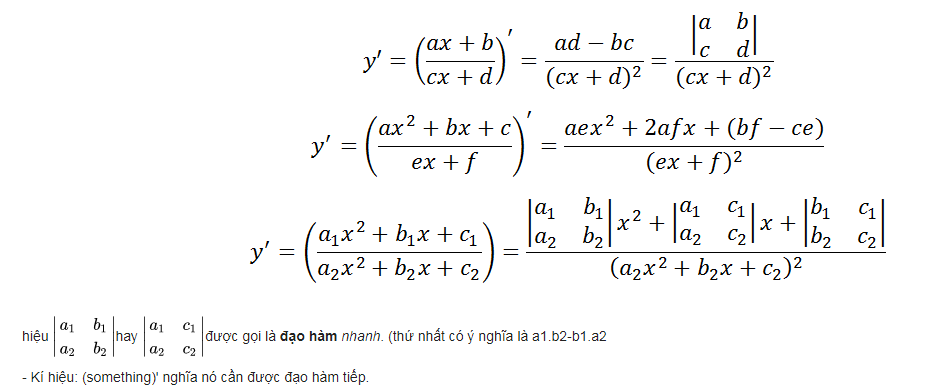
(u1+u2+…+un)′=u1′+u2′+…+un′.
- Hệ quả 1: Nếu k là một hằng số thì: (ku)’ = ku’.
- Hệ quả 2: (1v)′=––v′v2,(v(x)≠0)
(u.v.w)′=u′.v.w+u.v′.w+u.v.w′
2.4. Đạo hàm của hàm hợp
Cho hàm số y = f(u) với u = u(x) thì ta có: y′u=y′u.u′x.
Suy ra:
(un)=n.un–1.u′,n∈N∗.
(u−−√u)′=u′2u√u.
2.5. Bảng đạo hàm của hàm số có biến là x
(xα)’ = α.xα-1
(sin x)’ = cos x
(cos x)’ = – sin x
(tan x)’ = 1cos2x = 1 + tan2 x
(cot x)’ = −1sin2x = -(1 + cot2 x)
(logα x)’ = 1x.lnα
(ln x)’ = 1 x
(αx)’ = αx . lnα
Xem thêm : Bật mí công thức tính diện tích hình chữ nhật chính xác nhất
(ex)’ = ex
2.6. Bảng đạo hàm của hàm số có biến là u = f(x)
(uα)’ = α.u’.uα-1
(sin u)’ = u’.cos u
(cos u)’ = – u’.sin u
(tan u)’ = u′cos2u = u'(1 + tan2 u)
(cot u)’ = −usin2u = -u'(1 + cot2 x)
(logα u)’ = uu.lnα
(ln u)’ = u′u
(αu)’ = u’.αu.lnα
(eu)’ = u’.eu
2.7. Các công thức đạo hàm nâng cao
Ta cho hàm số y = f(x) có đạo hàm cấp n-1 kí hiệu f (n-1) (x) (với n ∈ N, n ≥ 4).
Nếu f (n-1) (x) có đạo hàm thì đạo hàm của nó được gọi là đạo hàm cấp n của y = f(x), y (n) hoặc f (n) (x).
f (n) (x) = [f (n-1) (x)]’
Công thức đạo hàm cấp cao:
Nếu m ≥ n thì ta được: (x m)(n) = m(m – 1)(m – 2)…(m – n + 1).xm – n
Còn nếu m ≤ n thì ta được: (x m)(n) = 0
3. Ví dụ minh họa cho các công thức tính đạo hàm
Tính đạo hàm của các hàm số sau:
- y = x3 – 2×2 + 3x +4
- y = sin x – cos x + tan x
- y = -x3 + 3×2 – 4x + 1 tại x0 = -1
Bài giải:
- a) Áp dụng công thức tính đạo hàm ta được:
y’ = ( x3 – 2×2 + 3x +4)’ = 3×2 – 4x + 3
- b) Áp dụng công thức tính đạo hàm ta được:
y’ = (sin x – cos x + tan x)’ = cos x + sin x + 1/cos2x
- c) Ta có: y’ = (-x3 + 3×2 – 4x + 1)’ = -3×2 + 6x – 4
Với x0 = -1 ta được: y’ = -3(-1)2 + 6(-1) – 4 = -13
Bài viết trên đây của chúng ta đã chia sẻ toàn bộ những công thức tính đạo hàm từ cơ bản đến nâng cao cho các bạn tham khảo, hy vọng qua bài viết các bạn sẽ nắm vững được các công thức và giải quyết bài tập một cách hiệu quả nhất. Chúc các bạn học tập vui vẻ!
Nguồn: https://www.nhomai.vn
Danh mục: Công Thức