Công thức tính diện tích hình thang học sinh nên biết

Hình thang là một hình khá phổ biến trong toán học và trong đời sống hàng ngày. Chu vi hình thang hay hình học phẳng nói chung cách tính khá đơn giản, chỉ cần cộng độ dài các cạnh lại với nhau, còn với diện tích hình thang thì công thức phức tạp hơn và khó tính hơn nhiều so với chu vi. Bài viết sau đây là tổng hợp công thức tính diện tích hình thang  ở các dạng phổ biến thường gặp nhất trong giải toán hình học.

1. Tìm hiểu chung về hình thang

Hình thang là một tứ giác lồi có hai cạnh đối song song với nhau và hai cạnh song song này được gọi là hai cạnh đáy, hai cạnh còn lại của hình thang được gọi là hai cạnh bên. Một số tính chất cơ bản của một hình thang như sau: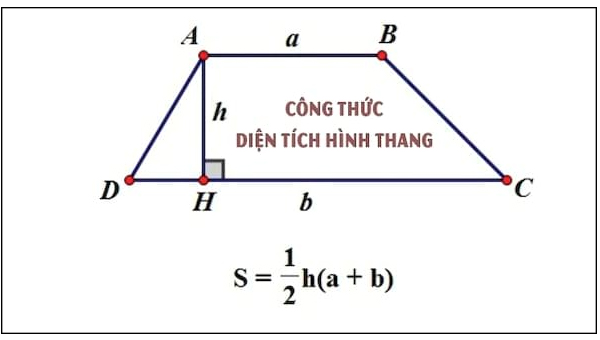

Bạn đang xem: Công thức tính diện tích hình thang học sinh nên biết

– Tính chất về góc: Trong hình thang, hai góc trong kề một cạnh bên của hình thang có tổng bằng 180 độ. Ví dụ: hình thang ABCD có AB//CD, AD và BC là hai cạnh bên thì góc BAD + ADC = 180 độ.

– Tính chất về cạnh:

+ Hai cạnh đáy hình thang bằng nhau thì hai cạnh bên của hình thang đó song song và bằng nhau.

+ Hình thang có hai cạnh bên song song với nhau thì chúng bằng nhau và hai cạnh đáy bằng nhau.

+ Trong một hình thang cân, hai đường chéo bằng nhau.

Cũng như hình tam giác có 7 dạng cơ bản khác nhau thì hình thang cũng có những dạng đặc biệt của nó:

– Hình thang vuông: hình thang vuông là hình thang thường nhưng có một góc vuông.

– Hình thang cân là hình thang có hai góc kề một đáy bằng nhau đồng thời hai cạnh bên của hình thang cân bằng nhau và không song song với nhau. Ví dụ hình thang ABCD có hai đáy AB//CD. Trong đó góc BAD= góc ABC và góc ADC = góc BCD; AD=BC.

– Hình bình hành cũng là một dạng đặc biệt của hình thang, là hình thang có hai cạnh đáy bằng nhau và hai cạnh bên song song và bằng nhau.

– Hình chữ nhật chính là dạng hình thang đặc biệt nhất, là hình thang vừa vuông vừa cân.

2. Công thức tính diện tích hình thang  ở nhiều dạng khác nhau

công thức tính diện tích hình thang nhìn chung ở các dạng đều có biến đổi giống nhau, tuy nhiên mỗi dạng chúng ta sẽ có những lưu ý nhỏ để tránh mắc lỗi trong giải toán tính diện tích hình thang.

2.1. Công thức tính diện tích hình thang thường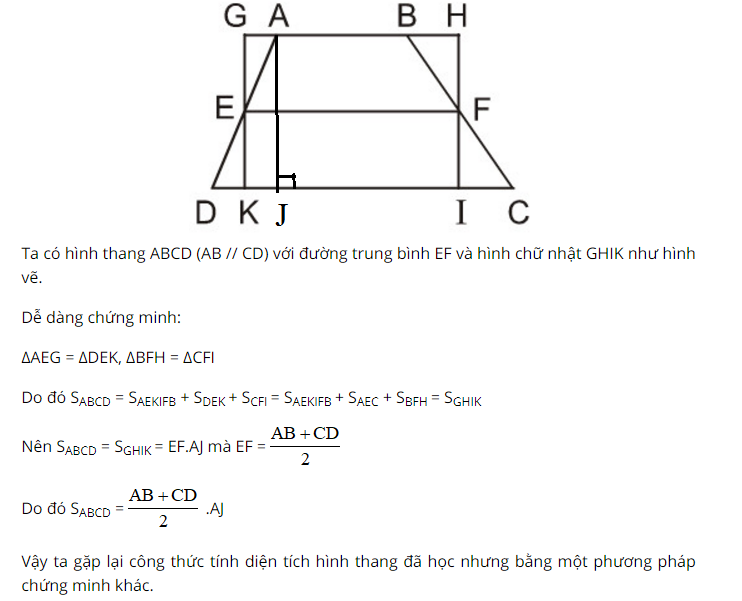

Xem thêm : Bật mí công thức tính điện năng tiêu thụ

Diện tích hình thang thường bằng trung bình cộng hai cạnh đáy nhân với chiều cao.

Công thức tính diện tích hình thang thường như sau: SABCD= [(a+b)h]/2

Trong đó:

– S là diện tích hình thang, đơn vị là cm2 ( dm2, m2)

– a là độ dài đáy nhỏ hình thang

– b là độ dài đáy lớn hình thang.

– h là chiều cao hình thang hạ từ đáy a xuống b hoặc ngược lại.

Để dễ nhớ công thức tính diện tích hình thang , ở trường tiểu học hoặc trung học cơ sở, thầy cô thường chỉ cho chúng ta cách nhớ công thức bằng một bài thơ ngắn như sau:

“Muốn tính diện tích hình thang

Đáy lớn đáy nhỏ ta đem cộng vào

Cộng vào nhân với chiều cao

Chia đôi lấy nửa thế nào cũng ra”

Bài thơ này tuy ngắn nhưng giải thích rõ ràng, đầy đủ và dễ hiểu công thức tính diện tích hình thang, bài thơ ngắn này là cách học kết hợp văn và toán, sự mềm mại và kho khan, tạo ra cách học vô cùng hiệu quả.

2.2. Công thức tính diện tích hình thang vuông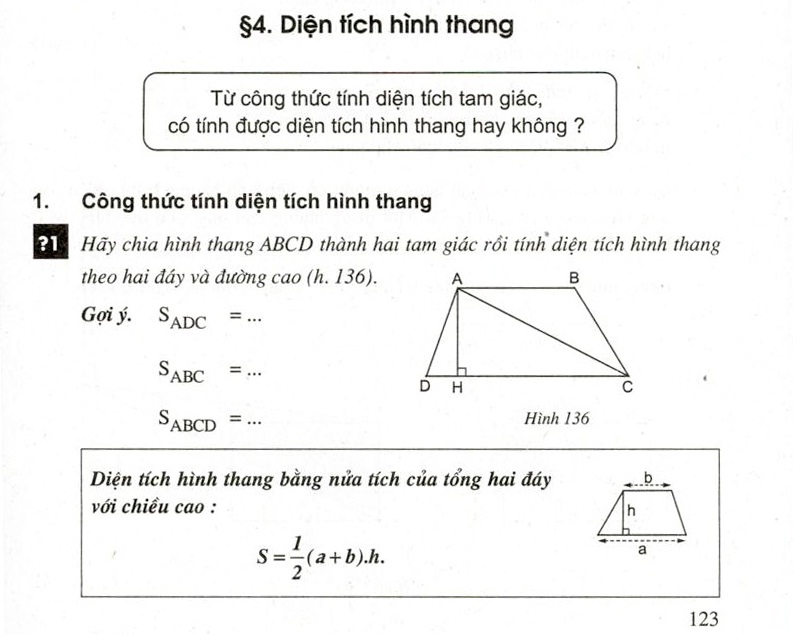

Đối với hình thang vuông, công thức tính diện tích cũng tương tự như hình thang thường, đó là bằng trung bình cộng của hai cạnh đáy nhân với chiều cao giữa hai đáy. Điểm đặc biệt cần chú ý ở đây là chiều cao của hình thang vuông cũng chính là cạnh bên vuông góc với cả hai đáy.

Xem thêm : Công thức tính diện tích hình bình hành

Công thức tính diện tích hình thang vuông ABCD vuông tại A và D:

SABCD= [(AB+CD)xAD]/2

Trong đó:

– AB và CD là độ dài hai cạnh đáy hình thang vuông.

– AD là độ dài cạnh bên vuông với hai đáy.

2.3. công thức tính diện tích hình thang cân

Với hình thang cân, ta có thể áp dụng công thức tính diện tích hình thang cân như hình thang thường là: : SABCD= [(a+b)h]/2.

Ví dụ: tính diện tích hình thang cân ABCD với AB//CD, AB= 5cm, CD= 7 cm; AH vuông góc với CD, AH = 6 cm. Tính diện tích hình thang cân.

Ta có AB//CD suy ra AB và CD là 2 đáy hình thang và AH là chiều cao hình thang.

Suy ra, diện tích hình thang ABCD là: SABCD= [(AB+CD)xAD]/2 = [(5+7)x6]/2=36 cm2.

Đối với những dạng hình thang đặc biệt còn lại như hình bình hành, hình chữ nhật thì chúng ta vẫn có thể sử dụng công thức tính diện tích hình thang thường hoặc sử dụng công thức tính diện tích của chính những hình này đều cho kết quả giống nhau:

– Công thức tính diện tích hình bình hành: S= axh. Trong đó a là độ dài cạnh đáy và h là chiều cao hình bình hành.

– Công thức tính diện tích hình chữ nhật: S= axb. Trong đó a là chiều dài và b là chiều rộng hình chữ nhật.

Như vậy, bài viết trên đã cung cấp những kiến thức chung về hình thang cũng như những công thức tính diện tích hình thang  ở các dạng hình thang khác nhau. Chúc các bạn học tập hiệu quả.

Nguồn: https://www.nhomai.vn
Danh mục: Công Thức